Division by zero algebra

A division by zero algebra $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\frac{0}{0}_D$ or $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_D$ is an algebraic structure where division by zero is possible, that is, there exists multiplicative inverses of zero elements.

As of 3 November 2016, there are two classes of division by zero algebra found so far ($\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{RPS}$ and $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{+}$).

Discovered on 17 October 2016, $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{RPS}$ demonstrates interesting algebraic properties resemble that of Rock Paper Scissors (RPS) commutative magmas, despite its relatively trivial addition structure. The generator equations for this class of division by zero algebra, provide some insights on a class of magmas (that lack division by zero) that generalise RPS to more than 3 types of moves and different winning conditions.

Discovered on 3 November 2016, $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{+}$is a division by zero near-semiring.

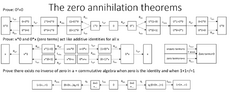
All known pathways to prove the annihilation property of additive identities using field axioms. L,R denote an element that demonstrate its properties only when operating on the (L)eft or (R)ight. id* and id+ are additive and multiplicative identities respectively, inv+ are additive inverses, Dist is distributivity, asso. is associativity and q is a multiplicative inverse of a zero. Zero expressions are terms consists of multiples of zero, such as 0x or x0.

Introduction: Zero annihilation theorems

Zero, being an additive identity, is forbidden to have multiplicative inverses under the ring axioms. This can be shown easily by the following proof (associativity is assumed):

Proof 1a: $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0*x=x*0=0$ (This shows $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0$ absorbs/annihilates all elements $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}x$, thus the existence of inverses will result in the trivial ring condition $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0=x$. Alternately, zero expressions such as $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0*x$ or $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}x*0$ are equivalent to $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0$)

$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white} \begin{align}0*x+x & =0*x+1*x & \text{(Left multiplicative identity)}\\ & = (0+1)*x & \text{(Right distributivity)}\\ & = 1*x & \text{(Left additive identity)}\\ & = x & \text{(Left multiplicative identity)}\\ & \Rightarrow 0x=0 & \text{(Cancellation or right additive inverse -x or associativity of +)} \end{align}$

$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}x*0=0$ can be shown similarly. In fact, the presence of the correct sided multiplicative inverses for an algebraic system where elemental properties defined for one side only is sufficient to show that zero expressions commute when multiplicative inverse of zero exists:

Proof 1b:

$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white} \begin{align}0*x & =0 & \text{(Proof 1a)}\\ 0*x*x^{-1} & = 0*x^{-1} & \text{(Right multiplicative inverse } x^{-1}\text{)}\\ q*0*x*x^{-1} & = q*0*x^{-1} & \text{(Left multiplicative inverse of zero q)}\\ q*0*x*x^{-1}*(x*0) & = q*0*x^{-1}(x*0) & \text{(}x*0 \in 1*1*x*0 & = 1*1*0 & \text{(left multiplicative identity)}\\ x*0 & = 0 & \text{(Left multiplicative identity)}\\ \end{align}$

In addition, the fact that $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0$ is commonly an additive identity in most algebraic systems means division by zero is generally incompatible with the ring axioms. Given the induction axiom of integers $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}1+1=2$$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white} \begin{align}0+0 & =0 & \text{(Additive identity)}\\ (0+0)*q & = 0*q & \text{(Right multiplicative inverse of zero q)}\\ 0*q+0*q & = 0*q & \text{(Right distributivity)}\\ 1+1 & = 1 \\ 2 & = 1 & \text{(Induction axiom)}\\ \end{align}$

Therefore trivial ring condition is resulted.

Therefore, in order to define nontrivial division by zero algebra, a selection of axioms need to be discarded, or be rearranged in a certain way so that the above proofs became impossible.

Properties

Zero term

Main article: Zero term

A zero term is a product of the form $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0*x$ or $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}x*0$ that is not equal to zero due to the requisite axioms that allow that to happen was discarded (usually the existence of additive inverses). Zero terms are very important in division by zero algebras as they control most of the addition structure of these algebras via the additive identity and their dominance properties. In division by zero algebra, an multiplicative identity $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}1$ becomes a zero term as zero inverses exist.

Zero terms are often idempotent, thus the study of division by zero algebras have close connection with the study of semigroups.

Examples

Generalised RPS magmas ($\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}M_{RPS}$) and RPS Division by zero algebra $\definecolor {GGG}{rgb}{0.5019607843137255,0.5019607843137255,0.5019607843137255}\pagecolor {GGG}\color {white}(\%_{RPS})$: Zero power laws

For rings, due to zero being both an identity and a successor element of the multiplicative identity $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}1$, preventing $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0$ from absorbing itself by breaking the proofs of the zero annihilation theorems reveals a recurrence relation that is normally buried within the absorbing properties of $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0$, known as zero power laws. These laws are the core theorems for this class of binary operator division by zero algebra. The laws controls the superiority of powers of zeros and zero terms under addition, and resembles a generalisation of RPS commutative magmas. In addition, a generalisation of these laws controls the structure of some generalised RPS magmas ($\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}M_{RPS}$), which are magmas obeying the RPS property shown below.

In RPS, given two elements $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a$ and $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}b$, ($\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a$)$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}b$ is said to (be dominated) dominate, or is (inferior)superior to ($\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}b$)$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a$ when

$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a+b=b$

and/or

$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}b+a=b$

Given a + Cayley table with rows and columns arranged from negative powers of zero to positive powers in ascending order down the table, each base property of zero and its powers (which are unconstrained) forms the ground level or generator equation of each law that controls one diagonal of the + Cayley table when it is multiplied successively by zero or its inverse(s), independent of other diagonals.

While the layout of the remaining subsections of the algebraic structure is quite general, as if the focus is on $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}M_{RPS}$, it should be note that there are only a few known set of examples of algebraic structure with the aforementioned generator equations that are members of $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{RPS}$ while most others are not even division by zero algebra due to the lack of zero elements after the construction. Conditions where the generalised RPS algebra is a member of $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{RPS}$ will be spelt out at the very end of this section.

Illustration of the main structural elements of a generalised RPS algebra (Gray shaded) composited with the ring of integers (off white grid at bottom right). The limit inferior is circled in thick blue, and the diagonals are marked with arrows. Starting with the generator equation, one can go up or down the series of relations by multiplying a or its inverse q. Each generator is said partition the algebra into cycles with cyclic order given by the rules of the generator equations.

Main diagonal

The generator equation is given by

$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0+0=a$

, where $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a \in M_{RPS}$ is free to be specified. The main diagonal corresponds to the tie cases of a generalised RPS cycle. If $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a$ is a power of $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0$, then the exponent is also known as the order of the RPS cycle. The usual RPS is given when $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a=0$. This is of order 1 and hence the tying elements are idempotents.

The RPS cycle can be of infinite order under the following conditions: If $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a$ is an additive identity $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}e$ in another ring, then $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}e$ represents the limiting inferior which is dominated by all other elements (in order to comply with the requirement of it being an additive identity). In such a scenario, it is possible to define the minus infinite power of the $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0$ in the algebra as equal to $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}e$. Similarly, if additive absorbers $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}u$ exists in $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}M_{RPS}$, then a limiting superior, which dominates all elements, can be defined as $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\lim_{R\rightarrow \infty}0^{R}=u$ or if the infinite element is unique, $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0^{\infty}=u$. The limit superior and limit inferior can be considered as the greatest element and least element of the algebra respectively.

1st subdiagonal

Typical RPS generated using the zero power laws. The main diagonal is marked in yellow, while the pale orange and light blue are the left and right 1st subdiagonals respectively. Note it loops around in finite structures like this. Also note this has no division by zero since 0 is one element short of being an identity.

There are two, the generator equations for each are given by

$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}1+0=b$

$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0+1=c$

, where $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}b,c \in M_{RPS}$ are free to be specified. These controls the winning rules, and often the length of the RPS cycle (the number of elements needed to step through in the RPS before it loops back to the start), and hence the direction of the RPS cycle for the left hand and right hand respectively (for noncommutative +). For elements of finite order, the subdiagonals can loop to the 2nd or even higher subdiagonals, but there is always a pair for each hand.

The 1st subdiagonal is significant as it proves that additive identities cannot exist in $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}M_{RPS}$ as there is always one element will be misaligned due to the power laws resulting in an element to be neutral to all except that specific element. For example, setting $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}c=1$ and demand commutativity results in $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0+0^2=0$ instead of $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0^2$, thus $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0$ ceased to be an additive identity.

To be consistent with the general formulation of the generator equations of the nth order diagonal, $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0^0=1$ is thus the natural choice.

Higher order subdiagonals

There are two for each order, each with a generator equation given by

$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0+0^{\pm n}=f$

$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0^{\pm n}+0=g$

for integers $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}n \neq 0,1$ and $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}f,g \in M_{RPS}$ free to be specified. These controls the RPS cycles for the nth nearest superior elements.

Symmetry

For each subdiagonal, if the element in the generator coincides (i.e. $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}b=c$,$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}f=g$ for all n), then the resulting algebra will be commutative.

Furthermore, if the aforementioned elements in all diagonals are defined in a fashion such that if some element $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}k_i$dominates $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}k_j$ implies $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}k_i$ dominates any $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}k_l$ with $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}j,l<i$ (that is, the RPS cycle has a strict total order induced by the winning rules being consistent throughout the cayley table), then all elements in the algebra will be left or right zeros, thus the + structure is isomorphic to the null semigroups.

The two sets of special cases corresponding to the cayley table that is isomorphic to one of the one sided null semigroups are the only ones that contains division by zero, and hence genuine members of the class $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{RPS}$, as one sided multiplicative inverse exists for all elements in the algebra, which are also one sided additive absorbers.

Only known cases of $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{RPS}$

Other algebraic properties of $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{RPS}$

The known members of $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{RPS}$ with n elements are constructed by having the + Cayley table to be isomorphic to the left or right null semigroup. The * Cayley table will usually be cyclic groups such as $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\mathbb{Z}$ or $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\mathbb{Z}/m\mathbb{Z}$ depending on the number of elements in the algebraic structure, thus giving a finite and an infinite example of the algebraic structure.

Due to the presence of left or right absorbers, addition is dominated by the leftmost or rightmost element regardless of the position of brackets. Therefore distributive laws and associativity of addition holds "trivially", and thus $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{RPS}$ forms a non abelian (for the +) near-field division by zero algebra.

Division by zero near-semiring $\definecolor {GGG}{rgb}{0.5019607843137255,0.5019607843137255,0.5019607843137255}\pagecolor {GGG}\color {white}(\%_{+})$

$\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{+}$ example: 0 act as an additive identity (blue) while both 0 and 1 act as left multiplicative identities (green). 0 has 1 as the unique right multiplicative inverse while the unique left multiplicative inverse of 1 is itself. The element a is a multiplicative absorber and is chosen to be an additive absorber for this example. The diagram on the right showed the relationship of the + Cayley table with the inverses act as maps between the entries (light gray is left multiplication, black is right multiplication). Note the right null subsemigroup in the * Cayley table (formedby 0 and 1) preventing collapse into the trivial ring from occurring.

By exploiting the property that $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}1$ is both an idempotent and an involution in most algebraic systems, it can be made into a one sided identity. Using this and setting an appropriate entry when zero and one are multiplied together, zero can absorb itself without collapsing the structure into the trivial ring.

The * Cayley table obtained is an idempotent semigroup.

The + Cayley table can then be populated using the RPS properties of the zero power laws. The result is isomorphic to the totally ordered semilattice, where the two element example and direct products of it are examples of a mutual distribution algebra where both operators distributive over each other.

The resulting structure is a left-near-semiring where the role of the annihilator is not taken by zero. Since a unique one sided multiplicative inverse exists for the additive identity $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}0$, it is a legitimate division by zero.

The structure however seemed relatively rigid. It was found that * associativity can only hold if the rows and columns corresponding to the element $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a$ is identically $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a$(i.e. a multiplicative absorber), and for + associativity to hold, $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a$must be an idempotent. Thus the only free equation is $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a+1$. If the result need to be equal to one of the existing elements, then either $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}1$ or $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}a$will be additive absorber. Therefore extension to larger size is not possible without breaking associativity. There are exactly 5 members in this class.

Absorber highlighted in bluish green or dark blue. Gray tiles are linked by the multiplicative inverses

Significance

While examples of $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{RPS}$ are rare and relatively trivial, as mentioned at the start of the section, the zero power laws that controls their structures are flexible and can be adapted to generate different classes of RPS magmas, and thus aid in the classification of them. By expanding the magma into a ringnoid like structure, any RPS can be made cyclic with the multiplication generates all elements in the RPS while addition governs the rules of the game.

The class of division by zero near-semiring $\definecolor{GGG}{RGB}{128,128,128}\pagecolor{GGG}\color{white}\%_{+}$ provide the first example of division by zero on an additive identity, thus a counterexample that additive identity implies the nonexistence of division by zero in associative ringnoids.